自動駕駛自誕生那天起，其志向便已立下，成為熟知城市每一處道路的“老司機”，成為乘客更安全、更舒適、更高效出行的“守護神”。在搞錢撈錢的大背景下，這個無私追求樸素得令人敬畏。 在自動駕駛的分工中，決策規劃將承擔上述志向實現的大部分工作，也因此被毫不吝嗇的稱為自動駕駛的大腦。決策規劃這塊網上已經有數量眾多的優秀科普文章，但他們都沒有長成《十一號組織》的樣子。抱著將所有自動駕駛知識都“擼一遍”的偉大理想，我決定用兩萬字簡述決策規劃的常用算法。

01 概述

1. 1 自動駕駛系統分類

自動駕駛系統沒有嚴謹的分類，但行業內普遍喜歡將自動駕駛系統區別為模塊化的和端到端的，圖1所示為兩者系統的原理框圖對比。

圖1 模塊化和端到端自動駕駛系統原理簡圖

1.1.1 模塊化自動駕駛系統

這是最經典也是業界采用最多的一種自動駕駛系統，也是最簡明清爽的一種結構，其作用是實時地求解出連續的控制輸出使得自動駕駛車輛可以安全地由初始位置行駛到目標位置。基于模塊化的思想，將自動駕駛系統劃分為三層：環境感知層、決策規劃層和控制執行層。每一層還可以劃分為不同的模塊，每個模塊還可以劃分為不同的子模塊……。

環境感知層就像是人的眼睛和耳朵，負責對外部環境進行感知并將感知結果送入決策規劃層。決策規劃層就像是人的大腦，在接收到感知信息后進行分析、決策，并生成加減速、變道、直行等控制命令。控制執行層就像人的雙手和雙腳，在接收到控制命令后控制執行器完成加速、轉向等操作。 模塊化自動駕駛系統中每一層都是關鍵和核心。但從實現自動駕駛功能的角度，環境感知層是基礎，決策規劃層是核心，控制執行層是保障。作為核心的決策規劃層帶著自動駕駛往“更安全、更舒適、更高效”的道路上狂奔，畢竟小小的失誤小則影響乘坐舒適性、通行效率，大則影響人身財產安全。

在模塊化自動駕駛系統中，不同團隊負責不同的模塊，可以實現更好的分工合作，從而提高開發效率。同時團隊內部可以對負責的模塊進行充分的評估，了解各模塊的性能瓶頸所在，從而讓我們能對最后的0.1%的不足有更清晰的認知，技術的迭代、更新。

缺點就是整個系統非常復雜、龐大、需要人工設計成百上千個模塊。二是對車載硬件計算能力要求高，如果越來越多的子模塊采用深度學習網絡，這將帶來災難性的計算需求爆炸。基于模塊化的自動駕駛系統，我們可能花10%的時間就實現了99.9%的問題，但我們還需要花90%的時間去解決最后0.1%的不足。 這個系統的難度之大，已經遠超一家公司的能力范圍，需要一個協作的生態。

1.1.2 端到端自動駕駛系統

術語端到端（End to End）來源于深度學習，指的是算法直接由輸入求解出所需的輸出，即算法直接將系統的輸入端連接到輸出端。2016年NVIDIA將端到端的深度學習技術應用在自動駕駛汽車之后，端到端自動駕駛迅速捕獲圈內一眾大佬的芳心，各種demo更是層出不窮。 所謂端到端自動駕駛是指車輛將傳感器采集到的信息（原始圖像數據、原始點云數據等），直接送入到一個統一的深度學習神經網絡，神經網絡經過處理之后直接輸出自動駕駛汽車的駕駛命令（方向盤轉角、方向盤轉速、油門踏板開度、制動踏板開度等）。

2016年NVIDIA發表了論文《End to End Learning for Self-Driving Cars》，拉開了端到端自動駕駛內卷的序幕。 論文首先展示了訓練數據的采集系統，如圖2所示。論文中只涉及了車道保持功能，因此訓練數據也只對攝像機的視頻數據和人類駕駛員操作方向盤的角度數據進行了采集。

圖2 數據采集系統框圖 三架攝像機安裝在采集車的擋風玻璃后面，并按照左中右依次布置，這樣布置是為了捕獲完整的前向路面信息。一臺NVIDIA DRIVETM PX被用來作為采集車的計算單元。攝像機生成的每一幀視頻數據（30FPS）都與人類駕駛員的轉向角度進行時間同步。 采集車最終在各式道路以及多樣照明和天氣條件組合下采集了72小時的駕駛數據。訓練數據包含視頻采樣得到的單一圖像，搭配相應的轉向命令。

但是只有來自人類駕駛員的正確數據是不足以完成訓練的，神經網絡還必須學習如何從任何錯誤中恢復，否則自動駕駛汽車就將慢慢偏移道路。因此訓練數據還擴充了額外的圖像，這些圖像顯示了遠離車道中心的偏離程度以及不同道路方向上的轉動。兩個特定偏離中心的變化圖像可由左右兩個攝像機捕獲。 訓練數據準備完畢之后，將其送入一個卷積神經網絡（CNN），訓練系統框圖如圖3所示。

圖3 訓練系統框圖 CNN計算一個被推薦的轉向命令，這個被推薦的轉向命令會與該圖像的期望命令相比較，CNN權重就會被調整以使其實際輸出更接近期望輸出。在這個框架中，只要提供足夠的訓練數據，即人類駕駛員駕駛攜帶有攝像頭的車輛累計駕駛大量的里程，再加上人為創造系統的“極限”道路狀態——偏離道路線的各種工況，CNN就會得到充分的訓練，而變得足夠強大。 一旦訓練完成，網絡就能夠從單中心攝像機（single center camera）的視頻圖像中生成轉向命令，圖4展示了這個配置。

圖4 訓練過的網絡用于從單中心前向攝像機中生成轉向命令

在端到端自動駕駛中，沒有人工設計的繁復規則，只需要極少的來自人類的訓練數據，深度學習神經網絡就會學會駕駛。且不用關心有沒有高精地圖覆蓋、此時是行駛在高速主干路還是城區道路、道路上車道線有沒有缺失等。 相比模塊化自動駕駛系統，端到端自動駕駛系統設計難度低，硬件成本小，還能借助數據的多樣性獲得不同場景下的泛用性。各方面條件得天獨厚，從理論層面看堪稱自動駕駛的終極夢想。

然而端到端深度學習神經網絡是一個完完全全的黑盒子，不具解釋分析性，可靠性、靈活性差，工程師們沒有辦法對它進行系統化的解釋分析，而是只能依靠推測和實驗進行調整。最終帶來的結果是安全難以得到保障，而自動駕駛最最關注的恰是安全。

比如端到端自動駕駛系統下汽車做出一個汽車減速左轉的行動，工程師們無法確定這是因為汽車看到行人，還是因為看到較遠處的紅燈。但是，在模塊化的自動駕駛系統下，由于多個識別系統嵌套，相對好理解到底汽車所做的每一個舉動背后的邏輯。

這也意味著，如果端到端系統出現問題時，工程師們并不能對其對癥下藥，做出合理的應對。更多情況下甚至只能簡單向模型灌注更多的數據，希冀它能在進一步的訓練中“自行”解決問題。這也會大大降低端到端自動駕駛系統原本開發簡單的優勢。

1.2 決策規劃分層架構

決策規劃的任務，就是在對感知到的周邊物體的預測軌跡的基礎上，結合結合自動駕駛車輛的和當前位置，對車輛做出最合理的決策和控制。 正如人的大腦又分為左腦和右腦、并負責不同的任務一樣，模塊化自動駕駛系統中決策規劃層也可以繼續細分為執行不同任務的子層。而這一分層設計最早其實是源自2007年舉辦的DAPRA城市挑戰賽，比賽中多數參賽隊伍都將自動駕駛系統的決策規劃方式包括三層：全局路徑規劃層（Route Planning）、行為決策層（Behavioral Layer）和運動規劃層（Motion Planning），如圖5所示。

圖5決策規劃分層架構

全局路徑規劃層聚焦在相對頂層的路徑規劃，聚焦在分鐘到小時級別的規劃。該層在接收到輸入的目的地信息后，基于存儲的地圖信息搜索出一條自起始點至目標點的一條可通過的路徑。如圖6所示，在藍色起點和黃色終點之間，黑色就是搜索出來的一條可通行的路徑，當然路徑不止一條，如何搜索出最優是下文將要介紹的內容。

在全局路徑規劃的時候，也可以基于地圖精度和豐富度，提前考慮道路曲率半徑、坡度等信息，來避免搜索出部分參數超出ODD要求的全局路徑。但是高度隨機的交通參與者、高度動態的交通流以及高度復雜的道路結構，全局路徑規劃是無法考慮周到的，因此還需要基于具體的行為決策進行后面的運動規劃，也就是局部路徑規劃。

行為決策層在收到全局路徑后，結合感知環境信息、交通規則信息、車輛狀態信息、駕駛場景信息等，推導判斷下一分鐘或下一秒時刻的情況，作出車道保持、車輛跟隨、車道變換和制動避撞等的適合當前交通環境的駕駛行為。如圖7所示，自車在檢測到前方存在低速行駛車輛，且右側車道滿足變道條件后，作出向右變道的駕駛行為決策。

運動規劃層也被稱為局部路徑規劃層，與全局路徑規劃聚焦在分鐘到小時級別的規劃不同，運動規劃聚焦在毫秒級到秒級的規劃。規劃的時候，根據輸入的行為決策信息、結合車輛實時位姿信息、局部環境信息、全局路徑參考信息等，在“安全、舒適、效率”的精神引領下，規劃生成一條滿足特定約束條件的平滑軌跡軌跡（包括行駛軌跡、速度、方向等），并輸入給控制執行層。 如圖8所示，在車輛收到行為決策層的左變道指令后，主車基于各種信息規劃出幾條可行的路徑，如何規劃出最優的路徑也是下文要介紹的內容。

全局路徑規劃與運動規劃作為兩個層級的不同規劃，現將其特點匯總為表1。

表1 全局路徑規劃與運動規劃特點對比

02 全局路徑規劃常用算法

正菜之前，我們先來了解一下圖（包括有向圖和無向圖）的概念。圖是圖論中的基本概念，用于表示物體與物體之間存在某種關系的結構。在圖中，物體被稱為節點或頂點，并用一組點或小圓圈表示。節點間的關系稱作邊，可以用直線或曲線來表示節點間的邊。

如果給圖的每條邊規定一個方向，那么得到的圖稱為有向圖，其邊也稱為有向邊，如圖9所示。在有向圖中，與一個節點相關聯的邊有出邊和入邊之分，而與一個有向邊關聯的兩個點也有始點和終點之分。相反，邊沒有方向的圖稱為無向圖。

圖9 有向圖示例

數學上，常用二元組G =（V，E）來表示其數據結構，其中集合V稱為點集，E稱為邊集。對于圖6所示的有向圖，V可以表示為{A，B，C，D，E，F，G}，E可以表示為{，，，，，，}。表示從頂點A發向頂點B的邊，A為始點，B為終點。

在圖的邊中給出相關的數，稱為權。權可以代表一個頂點到另一個頂點的距離、耗費等，帶權圖一般稱為網。

在全局路徑規劃時，通常將圖10所示道路和道路之間的連接情況，通行規則，道路的路寬等各種信息處理成有向圖，其中每一個有向邊都是帶權重的，也被稱為路網（Route Network Graph）。

那么，全局路徑的規劃問題就變成了在路網中，搜索到一條最優的路徑，以便可以盡快見到那個心心念念的她，這也是全局路徑規劃算法最樸素的愿望。而為了實現這個愿望，誕生了Dijkstra和A*兩種最為廣泛使用的全局路徑搜索算法。

2.1Dijkstra算法

戴克斯特拉算法（Dijkstra’s algorithm）是由荷蘭計算機科學家Edsger W. Dijkstra在1956年提出，解決的是有向圖中起點到其他頂點的最短路徑問題。

假設有A、B、C、D、E、F五個城市，用有向圖表示如圖11，邊上的權重代表兩座城市之間的距離，現在我們要做的就是求出起點A城市到其它城市的最短距離。

圖11 五個城市構建的有向圖

用Dijkstra算法求解步驟如下：

（1）創建一個二維數組E來描述頂點之間的距離關系，如圖12所示。E[B][C]表示頂點B到頂點C的距離。自身之間的距離設為0，無法到達的頂點之間設為無窮大。

圖12 頂點之間的距離關系

（2）創建一個一維數組Dis來存儲起點A到其余頂點的最短距離。一開始我們并不知道起點A到其它頂點的最短距離，一維數組Dis中所有值均賦值為無窮大。接著我們遍歷起點A的相鄰頂點，并將與相鄰頂點B和C的距離3（E[A][B]）和10（E[A][C]）更新到Dis[B]和Dis[C]中，如圖13所示。這樣我們就可以得出起點A到其余頂點最短距離的一個估計值。

圖13 Dis經過一次遍歷后得到的值

（3）接著我們尋找一個離起點A距離最短的頂點，由數組Dis可知為頂點B。頂點B有兩條出邊，分別連接頂點C和D。因起點A經過頂點B到達頂點C的距離8（E[A][B] + E[B][C] = 3 + 5）小于起點A直接到達頂點C的距離10，因此Dis[C]的值由10更新為8。同理起點A經過B到達D的距離5（E[A][B] + E[B][D] = 3 + 2）小于初始值無窮大，因此Dis[D]更新為5，如圖14所示。

圖14Dis經過第二次遍歷后得到的值

（4）接著在剩下的頂點C、D、E、F中，選出里面離起點A最近的頂點D，繼續按照上面的方式對頂點D的所有出邊進行計算，得到Dis[E]和Dis[F]的更新值，如圖15所示。

圖15 Dis經過第三次遍歷后得到的值

（5）繼續在剩下的頂點C、E、F中，選出里面離起點A最近的頂點C，繼續按照上面的方式對頂點C的所有出邊進行計算，得到Dis[E]的更新值，如圖16所示。

圖16 Dis經過第四次遍歷后得到的值

（6）繼續在剩下的頂點E、F中，選出里面離起點A最近的頂點E，繼續按照上面的方式對頂點E的所有出邊進行計算，得到Dis[F]的更新值，如圖17所示。

圖17 Dis經過第五次遍歷后得到的值

（7）最后對頂點F所有點出邊進行計算，此例中頂點F沒有出邊，因此不用處理。至此，數組Dis中距離起點A的值都已經從“估計值”變為了“確定值”。

基于上述形象的過程，Dijkstra算法實現過程可以歸納為如下步驟：

（1）將有向圖中所有的頂點分成兩個集合P和Q，P用來存放已知距離起點最短距離的頂點，Q用來存放剩余未知頂點。可以想象，一開始，P中只有起點A。同時我們創建一個數組Flag[N]來記錄頂點是在P中還是Q中。對于某個頂點N，如果Flag[N]為1則表示這個頂點在集合P中，為1則表示在集合Q中。

（2）起點A到自己的最短距離設置為0，起點能直接到達的頂點N，Dis[N]設為E[A][N]，起點不能直接到達的頂點的最短路徑為設為∞。

（3）在集合Q中選擇一個離起點最近的頂點U（即Dis[U]最小）加入到集合P。并計算所有以頂點U為起點的邊，到其它頂點的距離。例如存在一條從頂點U到頂點V的邊，那么可以通過將邊U->V添加到尾部來拓展一條從A到V的路徑，這條路徑的長度是Dis[U]+e[U][V]。如果這個值比目前已知的Dis[V]的值要小，我們可以用新值來替代當前Dis[V]中的值。

（4）重復第三步，如果最終集合Q結束，算法結束。最終Dis數組中的值就是起點到所有頂點的最短路徑。

2.2A*算法

1968年，斯坦福國際研究院的Peter E. Hart, Nils Nilsson以及Bertram Raphael共同發明了A*算法。A*算法通過借助一個啟發函數來引導搜索的過程，可以明顯地提高路徑搜索效率。

下文仍以一個實例來簡單介紹A*算法的實現過程。如圖18所示，假設小馬要從A點前往B點大榕樹底下去約會，但是A點和B點之間隔著一個池塘。為了能盡快提到達約會地點，給姑娘留下了一個守時踏實的好印象，我們需要給小馬搜索出一條時間最短的可行路徑。

A*算法的第一步就是簡化搜索區域，將搜索區域劃分為若干柵格。并有選擇地標識出障礙物不可通行與空白可通行區域。一般地，柵格劃分越細密，搜索點數越多，搜索過程越慢，計算量也越大；柵格劃分越稀疏，搜索點數越少，相應的搜索精確性就越低。

如圖19所示，我們在這里將要搜索的區域劃分成了正方形（當然也可以劃分為矩形、六邊形等）的格子，圖中藍色格子代表A點（小馬當前的位置），紫色格子代表B點（大榕樹的位置），灰色格子代表池塘。同時我們可以用一個二維數組S來表示搜素區域，數組中的每一項代表一個格子，狀態代表可通行和不可通行。

圖19 經過簡化后的搜索區域

接著我們引入兩個集合OpenList和CloseList，以及一個估價函數F = G + H。OpenList用來存儲可到達的格子，CloseList用來存儲已到達的格子。G代表從起點到當前格子的距離，H表示在不考慮障礙物的情況下，從當前格子到目標格子的距離。F是起點經由當前格子到達目標格子的總代價，值越小，綜合優先級越高。

G和H也是A*算法的精髓所在，通過考慮當前格子與起始點的距離，以及當前格子與目標格子的距離來實現啟發式搜索。對于H的計算，又有兩種方式，一種是歐式距離，一種是曼哈頓距離。

歐式距離用公式表示如下，物理上表示從當前格子出發，支持以8個方向向四周格子移動（橫縱向移動+對角移動）。

曼哈頓距離用公式表示如下，物理上表示從當前格子出發，支持以4個方向向四周格子移動（橫縱向移動）。這是A*算法最常用的計算H值方法，本文H值的計算也采用這種方法。

現在我們開始搜索，查找最短路徑。首先將起點A放入到OpenList中，并計算出此時OpenList中F值最小的格子作為當前方格移入到CloseList中。由于當前OpenList中只有起點A這個格子，所以將起點A移入CloseList，代表這個格子已經檢查過了。

接著我們找出當前格子A上下左右所有可通行的格子，看它們是否在OpenList當中。如果不在，加入到OpenList中計算出相應的G、H、F值，并把當前格子A作為它們的父節點。本例子，我們假設橫縱向移動代價為10，對角線移動代價為14。

我們在每個格子上標出計算出來的F、G、H值，如圖20所示，左上角是F，左下角是G，右下角是H。通過計算可知S[3][2]格子的F值最小，我們把它從OpenList中取出，放到CloseList中。

圖20 第一輪計算后的結果

接著將S[3][2]作為當前格子，檢查所有與它相鄰的格子，忽略已經在CloseList或是不可通行的格子。如果相鄰的格子不在OpenList中，則加入到OpenList，并將當前方格子S[3][2]作為父節點。

已經在OpenList中的格子，則檢查這條路徑是否最優，如果非最優，不做任何操作。如果G值更小，則意味著經由當前格子到達OpenList中這個格子距離更短，此時我們將OpenList中這個格子的父節點更新為當前節點。

對于當前格子S[3][2]來說，它的相鄰5個格子中有4個已經在OpenList，一個未在。對于已經在OpenList中的4個格子，我們以它上面的格子S[2][2]舉例，從起點A經由格子S[3][2]到達格子S[2][2]的G值為20（10+10）大于從起點A直接沿對角線到達格子S[2][2]的G值14。顯然A經由格子S[3][2]到達格子S[2][2]不是最優的路徑。當把4個已經在OpenList 中的相鄰格子都檢查后，沒有發現經由當前方格的更好路徑，因此我們不做任何改變。

對于未在OpenList的格子S[2][3]（假設小馬可以斜穿墻腳），加入OpenList中，并計算它的F、G、H值，并將當前格子S[3][2]設置為其父節點。經歷這一波騷操作后，OpenList中有5個格子，我們需要從中選擇F值最小的那個格子S[2][3]，放入CloseList中，并設置為當前格子，如圖21所示。

圖21第二輪計算后的結果

重復上面的故事，直到終點也加入到OpenList中。此時我們以當前格子倒推，找到其父節點，父節點的父節點……，如此便可搜索出一條最優的路徑，如圖22中紅色圓圈標識。

圖22 最后計算得到的結果

基于上述形象的過程，A*算法實現過程可以歸納為如下步驟：

（1）將搜索區域按一定規則劃分，把起點加入OpenList。

（2）在OpenList中查找F值最小的格子，將其移入CloseList，并設置為當前格子。

（3）查找當前格子相鄰的可通行的格子，如果它已經在OpenList中，用G值衡量這條路徑是否更好。如果更好，將該格子的父節點設置為當前格子，重新計算F、G值，如果非更好，不做任何處理；如果不在OpenList中，將它加入OpenList中，并以當前格子為父節點計算F、G、H值。

（4）重復步驟（2）和步驟（3），直到終點加入到OpenList中。

2.3兩種算法比較

Dijkstra算法的基本思想是“貪心”，主要特點是以起點為中心向周圍層層擴展，直至擴展到終點為止。通過Dijkstra算法得出的最短路徑是最優的，但是由于遍歷沒有明確的方向，計算的復雜度比較高，路徑搜索的效率比較低。且無法處理有向圖中權值為負的路徑最優問題。

A*算法將Dijkstra算法與廣度優先搜索（Breadth-First-Search，BFS）算法相結合，并引入啟發函數（估價函數），大大減少了搜索節點的數量，提高了搜索效率。但是A*先入為主的將最早遍歷路徑當成最短路徑，不適用于動態環境且不太適合高維空間，且在終點不可達時會造成大量性能消耗。

圖24是兩種算法路徑搜索效率示意圖，左圖為Dijkstra算法示意圖，右圖為A*算法示意圖，帶顏色的格子表示算法搜索過的格子。由圖23可以看出，A*算法更有效率，手術的格子更少。

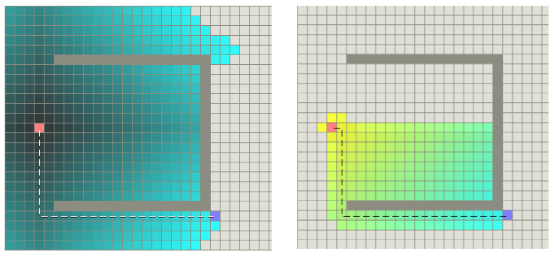
圖23 Dijkstra算法和A*算法搜索效率對比圖（圖片來源：https://mp.weixin.qq.com/s/myU204Uq3tfuIKHGD3oEfw）

03 行為決策常用算法

作為L4級自動駕駛的優秀代表Robotaxi，部分人可能已經在自己的城市欣賞過他們不羈的造型，好奇心強烈的可能都已經體驗過他們的無人“推背”服務。作為一個占有天時地利優勢的從業人員，我時常在周末選一個人和的時間，叫個免費Robotaxi去超市買個菜。

剛開始幾次乘坐，我的注意力全都放在安全員的雙手，觀察其是否在接管；過了一段時間，我的注意力轉移到中控大屏，觀察其夢幻般的交互方式；而現在，我的注意力轉移到了智能上，觀察其在道路上的行為決策是否足夠聰明。 而這一觀察，竟真總結出不少共性問題。比如十字路口左轉，各家Robotaxi總是表現的十分小心謹慎，人類司機一腳油門過去的場景，Robotaxi總是再等等、再看看。且不同十字路口同一廠家的Robotaxi左轉的策略基本一致，完全沒有人類司機面對不同十字路口、不同交通流、不同天氣環境時的“隨機應變”。

面對復雜多變場景時自動駕駛行為決策表現出來的小心謹慎，像極了人類進入一個新環境時采取的猥瑣發育策略。但在自動駕駛終局到來的那天，自動駕駛的決策規劃能否像人類一樣，在洞悉了人情社會的生活法則之后，做到“見人說人話”、“見人下飯”呢？ 在讓自動駕駛車輛的行為決策變得越來越像老司機的努力過程中，主要誕生了基于規則和基于學習的兩大類行為決策方法。